Zu-Haus-Gemachtes | Nr. 118

von Sarah und Piet | 08.06.2020, 10:27 Uhr

Hallo
dass wir uns nochmals melden, ist „Piets Schuld“. Schule ist ja wieder, auch mit Funktionen. Piet hat mich gefragt,

ob das mit quadratischen Funktionen genauso ist wie mit linearen Funktionen.

Das, was Piet jetzt weiß, hier für alle zusammengefasst:

Wenn gilt,
y = f(x) (mathematisch geschrieben) bedeutet: y ist ein Funktion von x (gesprochen)

y = f(x) ist eine ganz allgemeine Schreibweise, die für alle Funktionen gilt, wenn y von x abhängig ist oder mathematisch ausgedrückt … wenn y durch x bestimmt ist und abgebildet wird.

Deshalb wird y als eine abhängige Größe bezeichnet. Das x ist folglich eine unabhängige Größe.
Und da x und y verschiedene Werte einnehmen können, heißen sie Variablen.

Variablen sind also veränderliche Größen:
Das x ist die unabhängige Variable oder auch „Argument der Funktion“ genannt.
Und y ist die abhängige Variable oder auch „Funktionswert“ genannt..

In unserem linearen Beispiel mit den Crèpes lautetet eine konkrete Funktion: y =3*x + 6
Werden in unserem Beispiel die x-Werte mit den zugehörigen berechneten y-Werten in ein Koordinatensystem eingetragen, dann ergeben* lineare Funktionen immer eine Linie*.

Lineare Funktionen werden mathematisch allgemein gütig so geschrieben
y = f(x) = m*x + n
In unserem Beispiel ist m = 3 und n = 6, also y =3*x + 6

Wie ist das aber bei quadratischen Funktionen?

Genau wie bei linearen Funktionen gilt: y = f(x). y ist abhängig von x. Das x ist die unabhängige Variable oder auch das Argument der Funktion. Und y ist die abhängige Variable oder der Funktionswert.
Bei allen quadratischen Funktionen kommt immer das x als Quadrat vor:
Also x*x. Oder anders geschrieben: x*x = x2

Quadratische Funktionen werden mathematisch allgemein gütig so geschrieben:
y = f(x) = ax2 + bx + c

Zum Beispiel ist bei einer quadratischen Funktion: a = 3, b = 2 und c = 4, also y = 3×2 + 2x + 4

Für das Begreifen von mathematischen Funktionen ist wichtig – egal ob lineare, quadratische oder höhere Funktionen:

Der Funktionswert y ist immer abhängig von x.

Alle x-Werte sind durch den konkreten funktionalen Zusammenhang (wie bei unserem Beispiel: dass jeder 3 Crèpes isst) eindeutig einem Funktionswert y zugeordnet. Mathematisch gesagt: Jeder mögliche x-Wert wird eindeutig auf einen entsprechenden Funktionswert y abgebildet.

Euch viel Erfolg mit Funktionen …
von Piet und Sarah

Zu-Haus-Gemachtes | Nr. 109

von Sarah und Piet | 18.05.2020, 15:22 Uhr

Hallo,
der letzte Teil unserer gemeinsamen linearen Funktionsbetrachtungen:

Was ist bei allen Funktionen sehr wichtig?

Wie bereits geschrieben: Piet hat etwas gebraucht, um über unser Crèpes-Beispiel diese Frage zu beantworten. Aber er hat es „kapiert” – sagt er. Und er hat es bewiesen, in dem er mir es wirklich gut erklären konnte.

Piets Erklärungen:
Minus zwei Gäste gibt es nicht! Das ist ja Quatsch!!!

Wenn „niemand kommen”, dann ist x = 0”. Oder es kommen so viele, wie eingeladen wurden oder um die Party gewusst haben und ohne Einladung einfach gekommen sind … (Piet sagte … Das sind die Immer-Dreisten). Allerhöchstens 30 Leute. Das bedeutet: x geht von Null bis 30. Und nicht weiter. Und bei y ist das dann auch so, weil ja y (die Anzahl der Crèpes) immer von x (Anzahl der Leute) abhängig ist.

Piets Antwort ist völlig richtig!
Und auf meine Frage wie klein oder wie groß denn y sein, kam die Antwort:
Das kleinste y: Das sind die 6 Crèpes vom Vortag. Selbst wenn niemand kommt und x = 0 ist, sind die da. Und wenn maximal 30 Leute da sind und 90 Crèpes (30*3) frisch gebacken werden, dann ist y = 96.

Unsere Crèpes-Beispiel hat ziemlich gut gezeigt, dass es wichtig ist, genau zu wissen, wie groß oder klein x sein kann – und welche Werte x nicht haben kann.

Mathematisch wird der x-Bereich als der Definitionsbereich einer Funktion bezeichnet. Und der y-Bereich (also der Bereich, der sich aus den verschiedenen x-Werten berechnen lässt) wird als der Wertebereich einer Funktion bezeichnet.

Jeden x-Wert aus dem Definitionsbereich einer Funktion ist ein y-Wert Wertebereich einer Funktion zugeordnet.

• Der Zusammenhang zwischen y und x wird mit der linearen Funktion y=3*x+6 ausgedrückt.
• Definitionsbereich dieser Funktion: kleinste Zahl von x = 0, größte Zahl von x = 30
• Wertebereich dieser Funktion: kleinste Zahl von y = 6, größte Zahl von y = 96
• jeden x-Wert ist ein y-Wert zugeordnet: z.B. x = 1 dann ist y = 9 || x = 11 dann ist y = 39

Und weil, es zu jedem x-Wert nur einen einzigen y-Wert gibt – wird mathematisch diese Zuordnung als eindeutige Zuordnung oder eindeutige Abbildung bezeichnet,

Geschafft!

Ganz ehrlich, wenn wir beide vor Wochen geahnt hätten, dass wir uns solange mit linearen Funktionen beschäftigen werden … Aber: Es hat uns beiden zusammen Spass gemacht. Piet hat gesagt: Ist auch schade, dass es zu Ende ist. War richtig cool. Ich habs wirklich kapiert. Vielleicht könnten wir mal wieder so was machen …

Fand ich gut. Und ich bin auch ziemlich stolz auf meinen kleinen, größer werdenden Bruder …

Machst gut, besser zusammen …
von Piet und Sarah

Zu-Haus-Gemachtes | Nr. 107

von Sarah und Piet | 14.05.2020, 17:14 Uhr

Hallo,
hat doch etwas länger gedauert. Auch weil Schule wieder offener ist. Jetzt die oft gestellte Frage:

Was bedeuten Nullstellen?

In unserem Fall sind die Nullstellen einer linearen Funktion gemeint.

Das hat Piet ziemlich schnell verstanden:
Nullstellen gibt es, wenn x = 0 ist. Oder wenn y = 0 ist.

In unserem praktischen Beispiel mit Piets Geburtsgästen (die alle drei Crèpes essen werden)
Anzahl der möglichen Geburtstagsgäste = x
Anzahl der zu backenden Crèpes = y

Was bedeutet das, wenn x = 0 ist?
Piet sagt: „Mist, niemand ist gekommen. Mann, ist das peinlich!“

Was bedeutet das, wenn y = 0 ist?
Piet sagt: „Wenn niemand kommt, müssen auch keine Crèpes gebacken werden.
Also wenn x = 0 ist, dann ist auch y = 0“.

Bei meiner Frage „Wie das ist mit dem 6 Crèpes vom Vortag?“

hat Piet ein bisschen Zeit zum Überlegen gebraucht. Er hat sich auch sein Koordinatensystem mit den beiden Funktionen angeschaut. Dann wollte er mir es „etwas umständlich erklären“.

Mein Tipp an Piet:
Schreib alles, was du weißt, doch einfach auf – als Funktionsgleichung (also die mit dem Gleichheitszeichen).

Piet hat dann verschiedene Schreibweisen gehabt. Nach gemeinsamen Nachdenken, was das Wichtigste in der Aussage ist, hier die letzte Fassung.

Die Piet auch so erklären konnte.

1. Funktion: y = 3*x

x = Anzahl der möglichen Geburtstagsgäste
y = Anzahl der frisch zu backenden Crèpes

Nullstellen-Berechnung:
x = 0 Das bedeutet: y = 3*0 -> y= 0 || Regel: Multiplikation mit einer 0 = 0
y = 0 Das bedeutet: 0 = 3*x -> x = 0/3 = 0 -> x = 0 || Regel: Division durch 0 = 0

Wenn x = 0, dann ist auch y = 0
Wenn y = 0, dann muss auch x = 0 sein!

2. Funktion: y = 3x + 6

x = Anzahl der möglichen Geburtstagsgäste
y = Anzahl der Crèpes (der frisch zu backenden + 6 Stück vom Vortag)

x = 0 -> Das bedeutet: y = 3*0 + 6 -> y = 0 + 6 = 6
Weil ja schon 6 Crèpes da sind. Also, wenn x = 0, dann ist y = 6

Aber was ist, wenn y = 0 gesetzt wird?
Wenn doch y = Anzahl der Crèpes (der frisch zu backenden + 6 Stück vom Vortag). Die 6 Crèpes sind immer da!

Wenn wir trotzdem y = 0 setzen. Wie groß ist dann x?
0 = 3*x + 6 | -> auf beiden Seiten 6 abziehen
(wenn auf beiden Seiten der Gleichung der selbe Wert abgezogen wird, dann bleibt die Gleichheit erhalten)

-6 = 3*x | -> beide Seiten der Gleichung durch 3 teilen ( weil wir wollen den Wert von x, nicht den Wert von 3*x)
(wenn beide Seiten der Gleichung durch den selben Wert geteilt werden, dann bleibt die Gleichheit erhalten)

-2 = x (klar, weil -6 durch 3 ist = -2 und 3*x durch 3 ist = x) Also, wenn y = 0, dann ist x = -2

Aber was bedeutet … x = -2 bei unserem Crèpes-Beispiel?
Wenn x die Anzahl der Gäste ist? Und wieso kann den y = 0 sein, wo doch 6 Crèpes da sind?

Was meint ihr? Habt ihr eine Idee?

Piet hat auch ein bisschen gebraucht …
Was bei allen Funktionen sehr wichtig, kommt in unserem letzen Teil.

Euch Spass auf der Suche nach -2 Gästen …
von Piet und Sarah

Zu-Haus-Gemachtes | Nr. 90

von Sarah und Piet | 02.05.2020, 13:14 Uhr

Crèpes futtern … und lineare Funktion in ein Koordinatensystem zeichnen

Hallo,
wir, Piet und ich, haben es doch noch geschafft, unsere Crèpe-Beispiel-Funktion in ein Koordinatensystem zu zeichnen.

Piet hat es absolut allein gemacht.

Nur zur Erinnerung:
Anzahl der möglichen Geburtstagsgäste = x
Anzahl der zu backenden Crèpes = y
Alle Gäste essen drei Crèpes
Vom Tag zuvor waren 5 Crèpes übrig (für diejenigen, die noch ein Crèpe mehr essen wollen):

Piet hatte herausbekommen,
dass die Anzahl der frisch zu backenden Crèpes immer von der Anzahl der Gäste abhängt
dass die Anzahl der frisch zu backenden Crèpes einfach zu berechnen ist, nämlich: y = 3x

Wenn man in einem y-x-Koordinaten-System zu jedem x-Wert den passenden y-Wert einzeichnet – ergibt diese Abhängigkeit oder Funktion eine Line. Deshalb wird diese Funktion als lineare Funktion bezeichnet.

In unserem Beispiel:
Die Anzahl der Gäste = x
wenn 2 Gäste kommen, dann ist x=2 -> Anzahl der frisch zu backenden Crèpes ist y=3*2 = 6
wenn 6 Gäste kommen, dann ist x= 6 -> Anzahl der frisch zu backenden Crèpes ist y=3*6 = 18
wenn 8 Gäste kommen, dann ist x= 8 -> Anzahl der frisch zu backenden Crèpes ist y=3*8 = 24
wenn 10 Gäste kommen, dann ist x= 10 -> Anzahl der frisch zu backenden Crèpes ist y=3*10 = 30
wenn 20 Gäste kommen, dann ist x= 20 -> Anzahl der frisch zu backenden Crèpes ist y=3*20 = 60

Diesen Zusammenhang kann mach auch so schreiben
Wenn x= 2, dann ist y=6
Wenn x= 6, dann ist y=18
Wenn x= 8, dann ist y=24
Wenn x= 10, dann ist y=30
Wenn x= 20, dann ist y=60

Wie viele Leute können zu Piets Geburtstag kommen, wenn Piet im Garten feiern will?
Von 1, 2, 3, 4, 5, 6 bis 35 Gäste vielleicht? Wenn der Garten sehr, sehr groß ist, dann passen bestimmt auch 500 oder 1.000 Gäste hinein. Aber das ist natürlich Quatsch. Bei 1.000 Gästen müssten ich und unsere Mutter 3.000 Crèpes backen. Nie würde ich da mitmachen!

Und auch Piet hat gesagt, so viele Freunde hat er überhaupt nicht. Er findet, wenn er jetzt die Funktion zeichnen soll, dass 15 Freunde schon cool sind. Als Piet sich den Maßstab überlegt hat – meinte er: Es sind 6 Crèpes vom Vortag übrig geblieben.

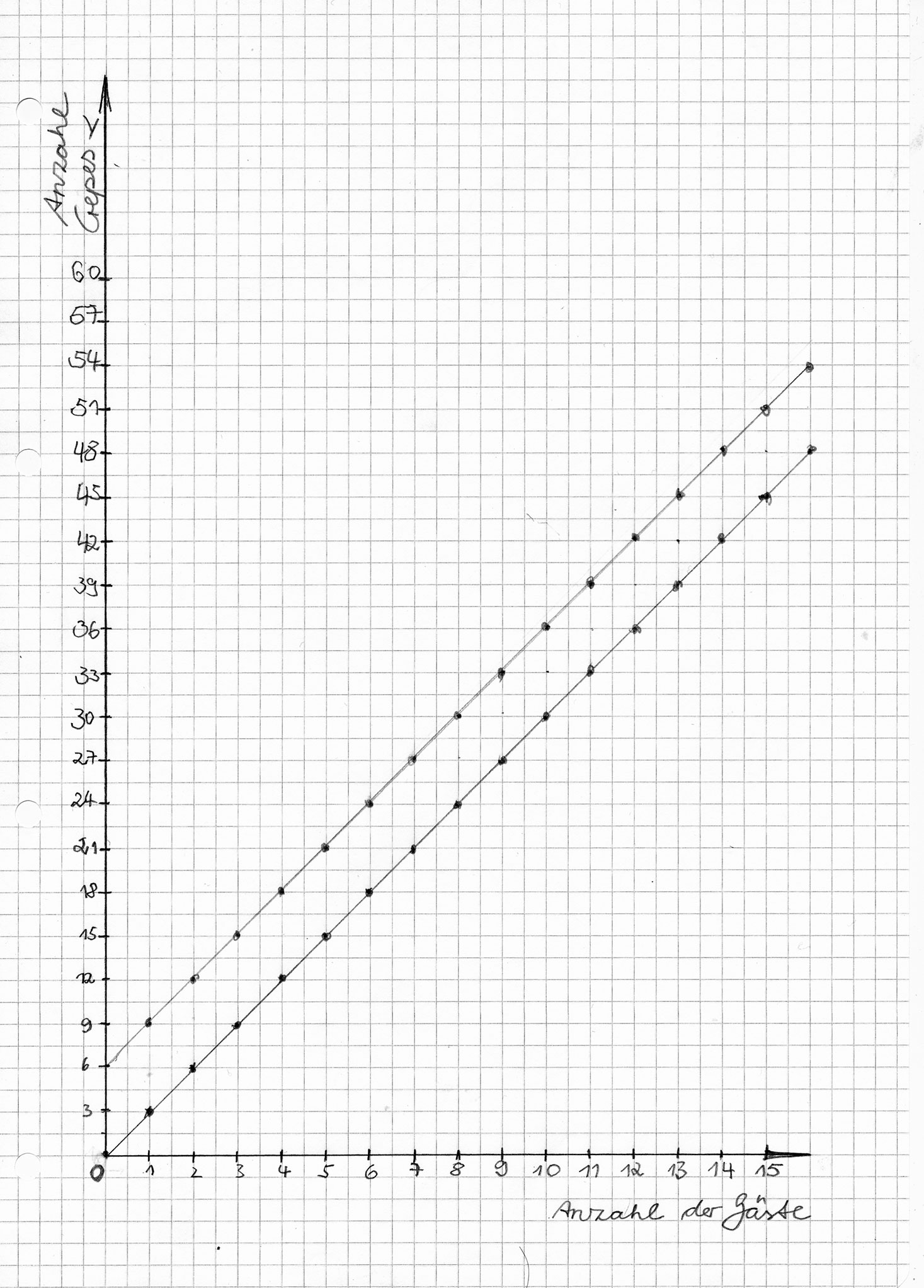
Das ist Piets Koordinatensystem:

Piet hat auf der X-Achse für jeden Gast zwei Kästchen genommen.
Und auf der y-Achse für je 3 Crèpes zwei Kästchen genommen.

Das ist der Grund, warum nicht 5 sondern 6 Crèpes vom Vortrag übrig bleiben mussten. Weil bei Piets Maßstab die Funktion mit den 6 Crèpes viel einfacher zu zeichnen ist.

Die untere Line ist y = 3x
-> das heißt: Alle essen jeweils 3 Crèpes. Es müssen 3 mal x Crèpes frisch gebacken werden.

Die obere Line ist y= 3x + 6
-> das heißt: Es sind vom Vortag noch 6 Crèpes da. Alle essen jeweils 3 Crèpes. Es müssen 3 mal x Crèpes frisch gebacken werden

Aber was bedeuten „die Nullstellen einer Funktion”?

Wir beide, Piet und ich, haben beschlossen, damit es nicht zu viel für Euch wird, dass wir hier erstmal ein Pause machen. Es wird aber nicht solange dauern wie beim letzten Mal, weil ich (Sarah) nicht jobben muss.

Ihr könnt ja überlegen, wie die Funktion heißen muss, wenn jeder 6 Crèpes essen möchte und wie die Funktion in Piets Koordinatensystem zu zeichnen ist. Vom Vortag sind keine Crèpes übrig geblieben.

Wir wünschen Euch viel Freude „beim Funktion-Zeichnen“
von Piet und Sarah

Zu-Haus-Gemachtes | Nr. 71

von Sarah und Piet | 18.04.2020, 15:56 Uhr

Crèpes futtern … und lineare Funktionen begreifen

Piet sollte beweisen, dass er über unser Crèpes-Beispiel „die mathematische Bedeutung von lineare Funktionen“ wirklich begriffen hat.

Hier meine Beweis-Frage, die ich Piet gestellt habe:

Angenommen wir haben schon einen Tag vor deiner Geburtstag-Party Crèpes gefuttert. Und es sind fünf Crèpes übriggeblieben. Die sind also schon da. Diese fünf Crèpes sind eine Reserve, falls jemand gern mehr als drei Crèpes essen möchte.

Hast Du eine Idee, wie dann die lineare Funktion aussehen muss, wenn y=Anzahl der Crèpes?

Piet war erst still. Er hat nachgedacht, vor sich hin gemurmelt.
So was wie „Bei 10 Leuten sind es 10 mal 3 = 30 plus 5 = 35, bei 20 Leuten sind es 20 mal 3 = 60 plus 5 = 65 …“
Und dann sagte Piet: Ich hab‘s.

y=Anzahl der Crèpes = 3x + 5

Stimmt! Perfekt. Piet grinste. Und ich war ganz schön stolz auf meinen Bruder (und auch auf mich.)

Dann wollte ich, dass wir die Funktion in ein Koordinatensystem zeichnen. Denn die Frage kennen alle in der 8. Klasse: Welche Nullstellen hat denn die Funktion? Da Piet es sich verdient hatte, sich mit seiner Play-Station zu beschäftigen, haben wir „Nullstellen und Koordinatensystem“ auf nächste Woche verschoben.

Mal sehen, wenn es gut geht, schreiben wir Euch wieder.
Bleibt dran
von Sarah

Zu-Haus-Gemachtes | Nr. 66

von Mascha | 15.04.2020, 14:01 Uhr

Hey,
ich hab das hier gelesen mit der „Nachhilfe“ in Mathe. Und ich geb auch Nachhilfe seit einiger Zeit – vor allem in Deutsch. Da ist mir aufgefallen, dass echt viele kids (und es ist egal wie alt sie sind) total oft Probleme haben in Deutsch mit dem Satzaufbau. Subjekt. Prädikat. Objekt.

Mir fällt das auf, weil ich früher auch eine Weile gebraucht hab, das schnell zu erfassen. Aber wenn meine Mutter dann bei den Hausaufgaben neben mir saß, dann fragte sie immer wieder:

Wer oder was tut etwas? Das ist das Subjekt.
Was tut der oder das? Das ist das Verb.

Ich hab das so oft von ihr gehört. Wer oder was tut etwas? Was tut der oder das? Bei allen möglichen Gelegenheiten. Ich konnte das singen. Aber es hat geholfen. Das funktioniert bei jedem Satz! Und das was „übrig bleibt“ ist dann das Objekt – aber dazu kann man dann wieder viel extra schreiben. Das ist so leicht zu merken… und hilft meist auch den kids in der Nachhilfe. Vor allem, wenn sie insgesamt Deutsch erst lernen mussten, weil es nicht ihre Muttersprache ist.
von Mascha

Hier noch zwei Beispiele:

Das Kind spielt Ball.
Wer oder was tut etwas: das Kind = Subjekt
Was tut das Kind: spielen = Verb
Was bleibt übrig: Ball = Objekt

Ehrlichkeit schafft Vertrauen.
Wer oder was tut etwas: Ehrlichkeit = Subjekt
Was tut Ehrlichkeit: schafft = Verb
Was bleibt übrig: Vertrauen = Objekt